《程序员的数学》读书笔记
《程序员的数学》这本书,主要介绍了程序员在编程中常用的数学知识和概念,以及它们在解决编程问题中的应用。
大纲
书中通过多个章节分别讲解了以下主题:
0的故事—无即是有:介绍了0在数学中的重要性,以及它在计数法和计算机科学中的作用。
逻辑—真与假的二元世界:讨论了逻辑在编程中的重要性,包括逻辑表达式、真值表、逻辑运算符的概念和应用。
余数—周期性和分组:探讨了余数的概念,以及如何利用余数进行分组和解决周期性问题。
数学归纳法—如何征服无穷数列:解释了数学归纳法的原理和应用,包括如何通过基底情况和归纳步骤来证明数学命题。
排列组合—解决计数问题的方法:介绍了排列和组合的概念,以及如何使用这些方法来解决计数问题。
递归—自己定义自己:讨论了递归的概念,包括递归定义、递归结构的发现和递归算法的设计。
指数爆炸—如何解决复杂问题:分析了指数爆炸问题,以及如何利用二分法查找和对数来处理这类问题。
不可解问题—不可解的数、无法编写的程序:探讨了不可解问题的概念,包括反证法、可数和不可数集合,以及停机问题的介绍。
总结篇:回顾了全书的内容,强调了数学在编程中的重要性,并鼓励读者在日常编程中运用数学思维。
附录部分讨论了机器学习的基础知识,包括感知器、神经网络、误差反向传播法、深度学习和强化学习的概念,以及人类在机器学习中的角色和决策问题。
书中通过各种实例和思考题来阐述这些概念,并鼓励读者通过学习这些数学知识来提升编程技能和解决问题的能力。
0的故事—无即是有
0在十进制计数法中用于占位,确保数值的正确表示。没有0,我们无法区分2503和253
0在二进制中更为重要,计算机使用二进制计数法,它只使用0和1两个数字。
0不仅用于占位,还有助于统一不同数值的表示方式,简化了数学规则和计数系统。
0在日常生活中的象征意义,如日程表中的“空计划”和药物的“无药效”的安慰剂,使用0来占位,就不需要定义更复杂的额外规则
这一章讲了:0作为一个数字在数学和编程中的重要性,以及它如何帮助我们简化问题和规则,使得计算机和人类能够有效地处理和表示数值。
逻辑——真与假的二元世界
计算机总是按照逻辑运行。
能够判断对错的陈述句叫作命题(proposition)。命题正确时,称该命题为“真”。反之,命题不正确时,称该命题为“假”。也将“真”称作 true,“假”称为 false。
在考虑规则时,确认有没有“遗漏”和“重复”是相当重要的。
- 没有“遗漏”,即具备完整性,由此明确该规则无论在什么情况下都能适用。
- 没有“重复”,即具备排他性,由此明确该规则不存在矛盾之处。
在遇到大问题时,通常将其分解为多个小问题。这时常用的方法就是检查它的完整性和排他性。
余数——周期性和分组
余数就是做除法运算时剩下的数
很多利用余数和奇偶性判断的例子
数学归纳法——如何征服无穷数列
数学归纳法要经过以下两个步骤进行证明
- 证明P(0)成立,这一步称作基底(base)
- 证明不论 k 为 0 以上的哪个整数,若 P(k) 成立,则 P(k+1) 也成立,这一步称作归纳(induction)
若步骤 1 和步骤 2 都能得到证明,就证明了“断言 P(n) 对于 0 以上的所有整数 n 都成立”。
这种数学归纳法的思路可以比喻为“推倒多米诺骨牌”。假设现在有很多多米诺骨牌排成一列。只要保证以下两个步骤,那么无论多米诺骨牌排得有多长最终都能倒下。
- 步骤1 确保让第 0 个多米诺骨牌(排头的多米诺骨牌)倒下
- 步骤2 确保只要推倒第 k 个多米诺骨牌,那么第 k+1 个多米诺骨牌也会倒下
熟练掌握数学归纳法的思路对于程序员来说是相当重要的
排列组合——解决计数问题的方法
计数时必须要注意的是“遗漏”和“重复”。
遗漏就是没有数全所有的数,有漏数的情况。换言之,就是“明明还有没数到的,却错认为数过了”。
重复则和“遗漏”恰恰相反,是将已经数了的,又多数了一次或几次。
植树问题: 在 10 米长的路上,从路的一端起每隔 1 米种 1 棵树,那么需要种多少棵树?
本题是非常著名的植树问题。有些人会下意识地计算 10 ÷ 1 = 10,认为只要 10 棵树就够了。不要忘记 0 这点很重要。像上述解答方法那样在纸上画图数数也是一种好方法。10 ÷ 1 的结果 10 并不是树的棵数,而是“树与树的间隔数”。
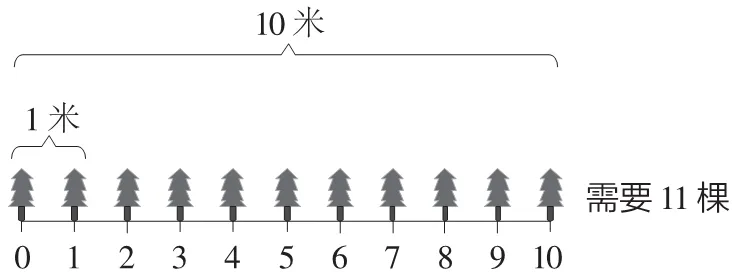
因此最终的答案是11。
这个问题跟数组计数从0开始很相似。
置换
将n个事物按顺序进行排列称为置换(substitution)
如果将 A, B, C 这 3 张牌按照 ABC, ACB, BAC 等顺序排列,那么共有多少种排法?
- 第 1 张牌(最左边的牌),从 A, B, C 中选出 1 张。即,第 1 张牌有 3 种选法。
- 第 2 张牌,从已选出的第 1 张牌以外的 2 张中选出 1 张。即,第 2 张牌与第 1 张牌的选法相对应,分别有 2 种选法。
- 第 3 张牌,从已选出的第 1、第 2 张牌以外的 1 张中选出 1 张(其实剩下的只有 1 张牌,因此只能选这张)。即,第 3 张牌与第 1、第 2 张牌的选法相对应,分别有 1 种选法。
最后的结果是3!表示3*2*1。
要注意 0 的阶乘 0! 不是 0,而被定义为 1。这是数学里的规定。
排列
从 n 个事物中取出一部分进行排列(permutation)。
你现在手上持有 A, B, C, D, E 共 5 张牌。要从这 5 张牌中取出 3 张牌进行排列。请问有多少种排法?
排列与置换相同,也是要考虑顺序的,唯一的区别是排列值需要一部分事物。
P(n,k)表示从n个事物中取k个进行排列:P(n,k) = n! / (n-k)!
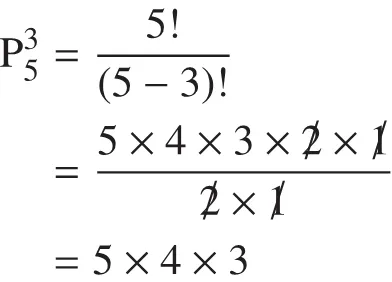
组合
置换和排列都需要考虑顺序,还有一种取法称为组合(combination)
设现在有 5 张牌 A, B, C, D, E。要从这 5 张牌中取出 3 张牌,并且不考虑它们的顺序,一共有多少种组合?
这里使用的先考虑顺序进行计数,然后除以重复度的方法,是计算组合时常用的计算方法。
C(n,k)表示从n个事物中取k个进行组合:C(n,k) = P(n,n) / P(k,k)

递归——自己定义自己
我们在解“6 层汉诺塔”时,先试着解出了稍为简单的 3 个圆盘的“3 层汉诺塔”。然后,为了找出更具有普遍性的解决办法,又使用了以下方法。
- 【使用递归来表示】找出借助“n-1 层汉诺塔”来解“n 层汉诺塔”的步骤。
- 【递推公式】使用“n-1 层汉诺塔”的移动次数来表示“n 层汉诺塔”的移动次数。
能将复杂问题转换为较为简单的同类问题,这就是递归的思维方式。
对于汉诺塔来说,就是将 n 层汉诺塔转换为 n-1 层汉诺塔的问题,即在问题中找出递归结构
如果找到了这种递归结构,接下来就根据递归结构建立递推公式。
找出递归结构并建立递推公式,是相当重要的一环。如果能够总结出解析式自然最为便捷,不过若找不到解析式,只建立递推公式也是非常有用的。因为它是得出具体数值的线索,同时也能帮我们把握问题的本质。
递归(recursion)和归纳(induction)在本质上是相同的,都是“将复杂问题简化”。
递归和归纳,只是方向不同。“从一般性前提推出个别性结论”的是递归的思想。而“从个别性前提推出一般性结论”的是归纳的思想。
面对递归问题,不要直接想第n层是什么数据,而应该想n-1、n-2...的数据。
指数爆炸——如何解决复杂问题
2^n当n线性增加时,数据会急速上升
二分法查找:利用指数爆炸进行查找
二分法查找(binary search)是在有序数据中找出目标数据时“总是判断目标数据所在范围内正中间数据”的方法。也叫作“二分法”“二分查找”。
二分法查找的关键在于,每判断 1 次就能筛选出近一半的查找对象。
对数是乘方的逆运算。再难以处理的庞大数值,它的对数都是更易处理的较小数值
不可解问题——不可解的数、无法编写的程序
本章首先介绍基础知识“反证法”和“可数”的概念。然后,向大家展示“不可解问题”。最后,以“停机问题”为例,具体地讲解不可解问题。
反证法,有时也被称为归谬法
- 首先,假设“命题的否定形式”成立。
- 根据假设进行论证,推导出矛盾 1 的结果。
你要请我喝一杯奶茶?
版权声明:自由转载-非商用-保持署名和原文链接。
本站文章均为本人原创,参考文章我都会在文中进行声明,也请您转载时附上署名。
